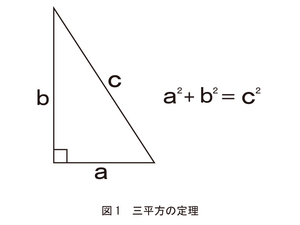
三 平方 の 定理 は ピタゴラス
ベクトルVector3ベクトルの (x *x+y* y+z* z) の平方根の長さを返しますmagnitudeはベクトルの長さを返す。Unity リファレンスこう書いてあります。なんのこっちゃってことですよね。一言でいうと、ベクトルを返して.

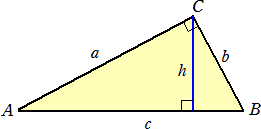
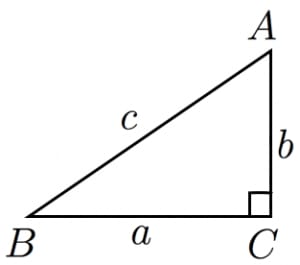
三 平方 の 定理 は ピタゴラス. 数学史から入る「三平方の定理」 「三平方の定理」は,いつ,どのようにして発見されたか ・・・・・・ 片野 善一郎;. 最高三 平方 の 定理 は ピタゴラス 三平方の定理 ピタゴラスの定理 わかる数学. はじめに 直角三角形の定理で、高校になってからもかなり活躍する定理をここで紹介します。その名も、三平方の定理(ピタゴラスの定理)です。 三平方の定理 まず図のような直角三角形ABCを描きます。 各頂点A、B、Cに対応する辺をそれぞれa、b、cと.
A 2 + b 2 = c 2 を満たす自然数の組 (a, b, c) をピタゴラス数またはピタゴラスの三つ組数 (Pythagorean triple) という。 特に、 a, b, c が互いに素であるピタゴラス数 (a, b, c) を原始的 (primitive) あるいは素 (coprime) であるといい、そのようなピタゴラス数は原始ピタゴラス数 (primitive Pythagorean. たとえば $6$ と $24$ をかけると平方数 $144=12^2$ となりますが、$6=2×3$、$24=2^3×3$ なので互いに素ではありません。これが $16×9=144$ であれば、$16=2^4$、$9=3^2$ で素因数の被りがないため、$16$ と $9$ は互いに素であり、かつそれぞれが平方. ブリタニカ国際大百科事典 小項目事典 - ピタゴラスの定理の用語解説 - 三平方の定理ともいう。直角三角形において,直角である頂角の対辺の長さの平方は,他の2辺の平方の和に等しいという定理。いま三角形 ABC において,∠C=∠R (直角) ,各頂角の対辺の長さをそれぞれ a,b,c とすれば a2.
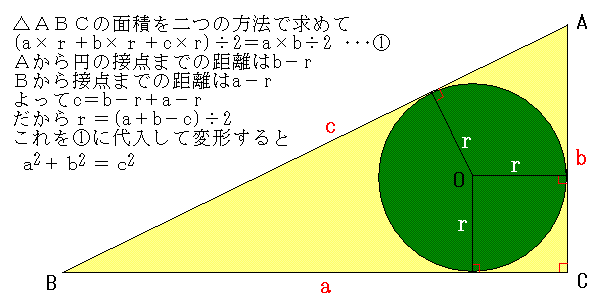
ピタゴラスの定理が有用なのは,定理の逆も成り立つからです。 ピタゴラスの定理の逆 三角形の三つの辺の長さをa,b,cとするとき,もしその間に, a 2 +b 2 =c 2 という関係が成り立つならば ,この三角形は,cという長さの辺に対する角が直角である. ピタゴラスの定理は、辺a、b、cの長さに関する方程式として書くことができ、多くの場合、ピタゴラスの方程式と呼ばれます。 a 2 + b 2 = c 2. ピタゴラスの定理の証明と無理量の発見 ・・・・・・ 上垣 渉 「三平方の定理の証明」の授業.
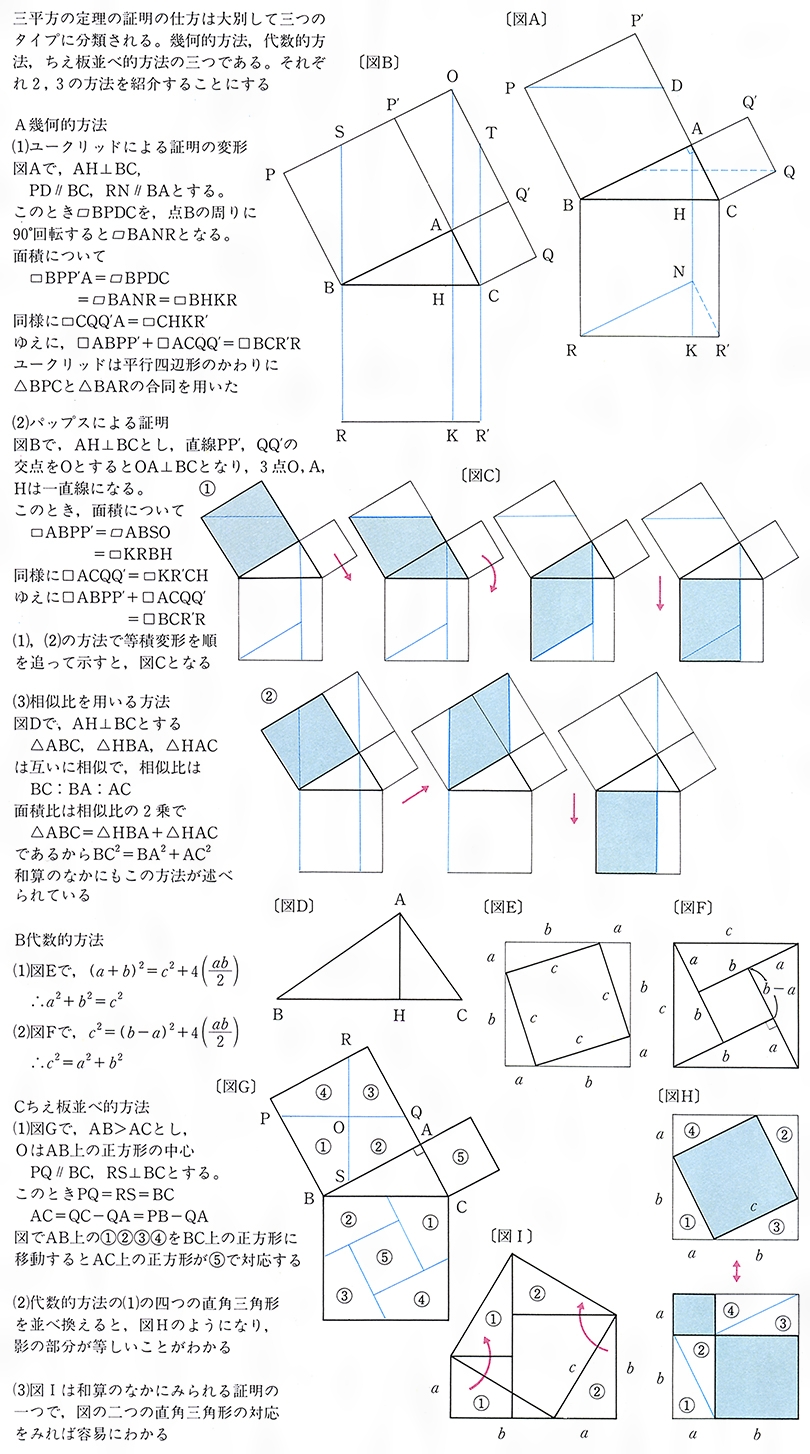
三平方の定理には数百もの証明方法があります。その中でも最も基本的で歴史の古い、ピタゴラスが考えた証明について説明します。 ①三平方の定理とは ②ピタゴラスの証明 ③その他の証明方法へ ①三平方の定理. 100+ EPIC Best三 平方 の 定理 証明 中学生 melan melani | 年7月26日日曜日 中学受験算数 三平方 ピタゴラス の定理を小学生向けに証明. 3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru.
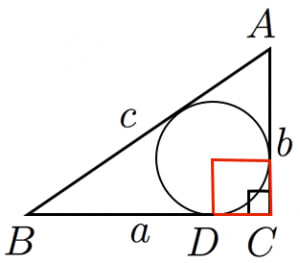
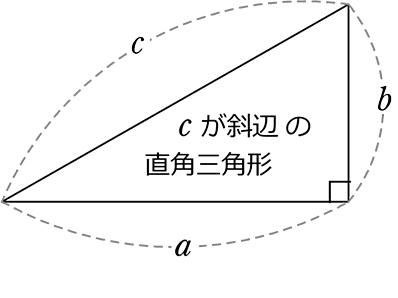
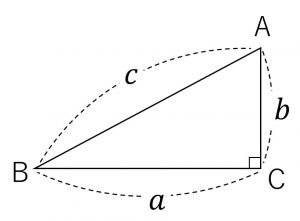
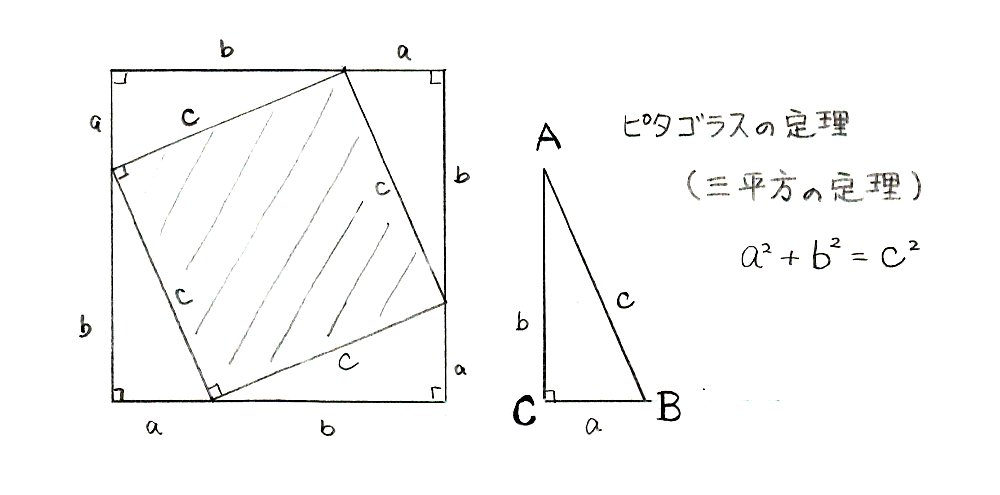
三平方の定理 の問題のわからないを5分で解決 映像授業のtry It Adqはd90の直角三角形またdqは三平方の定理により42 だから adqに三平方の定理を用いてaqエcm. 三平方の定理 1 三平方の定理 ここでは,直角三角形の辺の長さの関係について学習してみましょう。 三平方の定理(ピタゴラスの定理) 直角三角形の直角をはさむ2 辺の長さをa,bとし,斜辺の 長さをcとすると a2+b2=c2 が成り立つ。. が成り立ちます.(これを三平方の定理といいます.) これを用いて3辺の長さのうち2辺の長さが分かっているとき,残りの1辺の長さを求めることができます. 証明・・・証明の仕方は何十通り~何百通りあると言われています。中でも簡単そうなのは次.
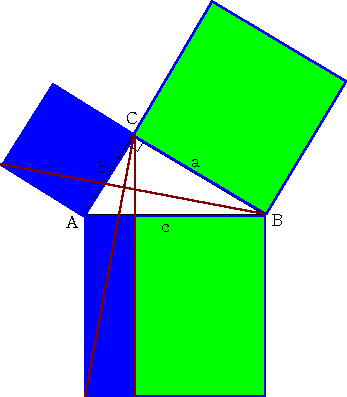
Zの素因数pが を満たすならば、2平方和定理よりp=a 2 +b 2 と表される。 フィボナッチの等式より、この形の素因数の積は、z=m 2 +n 2 と表される。 素因数の取り方より、mとnの偶奇性の異なる互いに素な整数として、ブラーマグプタの公式を満たす。. ピタゴラスの定理、ピタゴラス方程式 直角三角形に関して、最も長い一辺( 斜辺 ( しゃへん ) )の長さをz。それ以外の二辺をx、yとすると、三辺の長さの関係は、 x 2 + y 2 = z 2 (1) となる。 これは『ピタゴラスの定理』と呼ばれる。. 二次元での定理を三次元に拡張 1. はじめに 直角三角形で成り立つ三平方の定理(ピタゴラスの定理)というのはかなり有名です。 私たちはこの定理を三次元(立体)に拡張したときにどうなるのかというのに興味を持ち ました。.
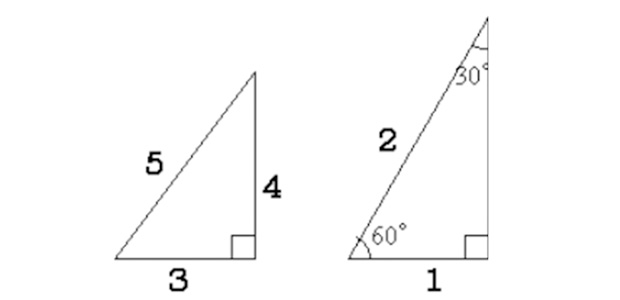
三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角二等辺三角形タイプです。 これは「正方形半分タイプ」という名前でも覚えておきましょう。. ピタゴラスの定理(別名三平方の定理) 斜辺の2乗=底辺の2乗+高さの2乗が成立します。 すなわち aの2乗=bの2乗+cの2乗 又は bの2乗=aの2乗+cの2乗 又は cの2乗=aの2乗+bの2乗 が成立すれば直角三角形です。. 三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが \(3cm\) と \(4cm\) の直角三角形の斜辺の長さを実際に測ってみると、\(5cm\) であることが分かります。.
超難問 ねこたさんのごった煮日和 三平方の定理ピタゴラスの定理の計算問題の解き方教えて どうもぺーたーだよ 中3数学では 三平方の定理ピタゴラスの定理 っていう単元を勉強するよ この章が終われば中3年の数学はほぼ終わりあともう少し頑張って勉強していこう. 三平方の定理による辺の長さの計算です。三平方の定理は、 直角三角形の三辺をa,b,cとする。斜辺(最も長い辺)をcとすると、 c² = a² + b² が成り立つ. (a) $(2x)^2 = 4x^2,$ $(2x+1)^2 = 4(x^2+x)+1$ から, 整数の平方を $4$ で割った余りは $0$ か $1$ のいずれかであることに注意する.
ピタゴラスの定理の覚え方としては、 斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。. *1 三平方の定理(ピタゴラスの定理)については、拙書『大人のための中学数学勉強法 』に詳しく書きました。一部を抜粋します。 三平方の定理(ピタゴラスの定理)の誕生秘話 ピタゴラスはギリシャのサモス島というところで生まれました。このサモス島のヘーラー神殿というところを散策. なぜ球の体積が4πr^3/3 https://youtu.be/l75rFXN9Gls 中学生の知識でオイラーの公式を理解しよう https://youtu.be/O5BLVlYgonc ブログ http.
三平方の定理(ピタゴラスの定理) 関連ページ 図形の面積を求める公式 三角形、平行四辺形、ひし形、台形、正六角形、円、扇形、楕円などの平面図形の面積を求めるときに使う公式についてまとめています。.
投稿1036

ピタゴラスの定理 Wikipedia

三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学
三 平方 の 定理 は ピタゴラス のギャラリー

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 ベネッセコーポレーション
ピタゴラスの定理 Wikipedia

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

三平方の定理 自動計算サイト
三平方の定理

ピタゴラスの定理

ピタゴラスの定理 Wikipedia
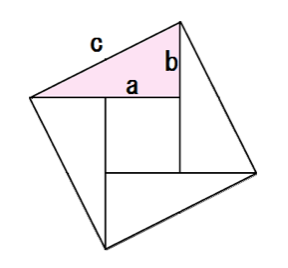
三平方の定理の4通りの美しい証明 高校数学の美しい物語

中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

ピタゴラスの定理 の証明アニメ4 バスカラ Youtube
名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 ひ ではじまるキーワード キーワード ピタゴラスの定理 公式と図形

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
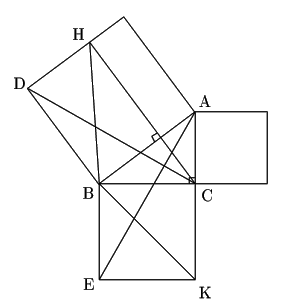
三平方の定理

コラム ピタゴラスの定理 江戸の数学

中学数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

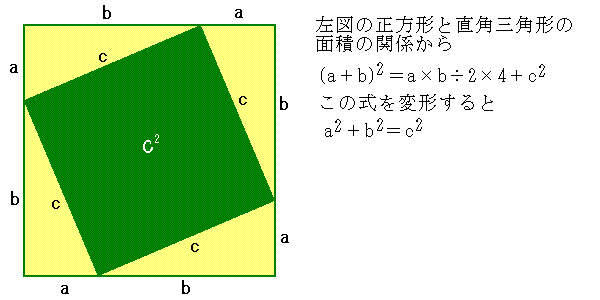
三平方の定理の証明 正方形の面積を使う方法 数学教材

中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook
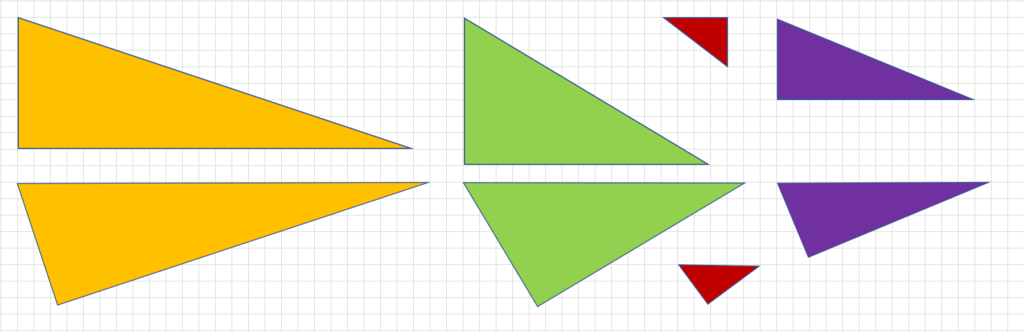
中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog
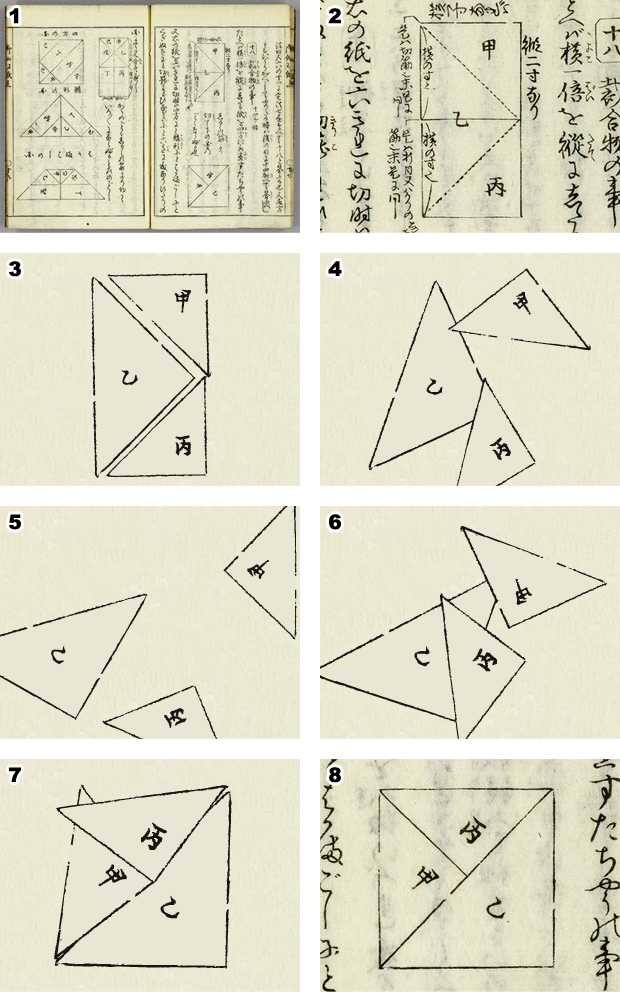
コラム ピタゴラスの定理 江戸の数学

三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
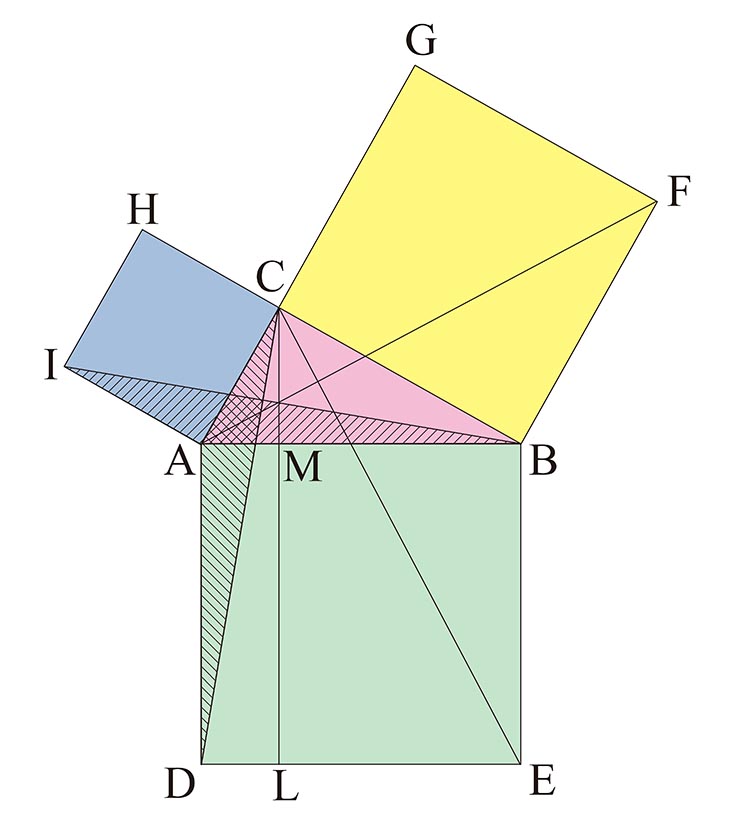
コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション
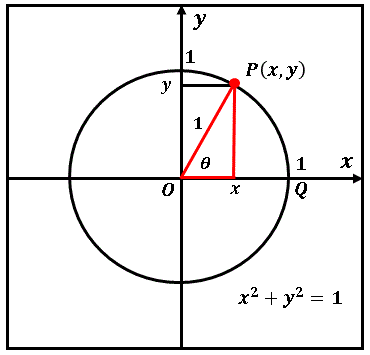
Excel Vba 数学実験室 ピタゴラスの定理と円の方程式

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生

ピタゴラスの定理 三平方の定理 ピタゴラスの定理

中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張
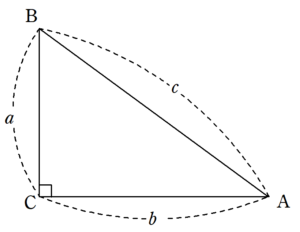
三平方の定理の証明 ピタゴラスの証明 Fukusukeの数学めも

三平方の定理 ピタゴラスの定理 東大合格コム

三平方の定理 がひと目で分かる展示が面白いと話題に 視覚的にわかる こういうのが学校にあったら ねとらぼ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
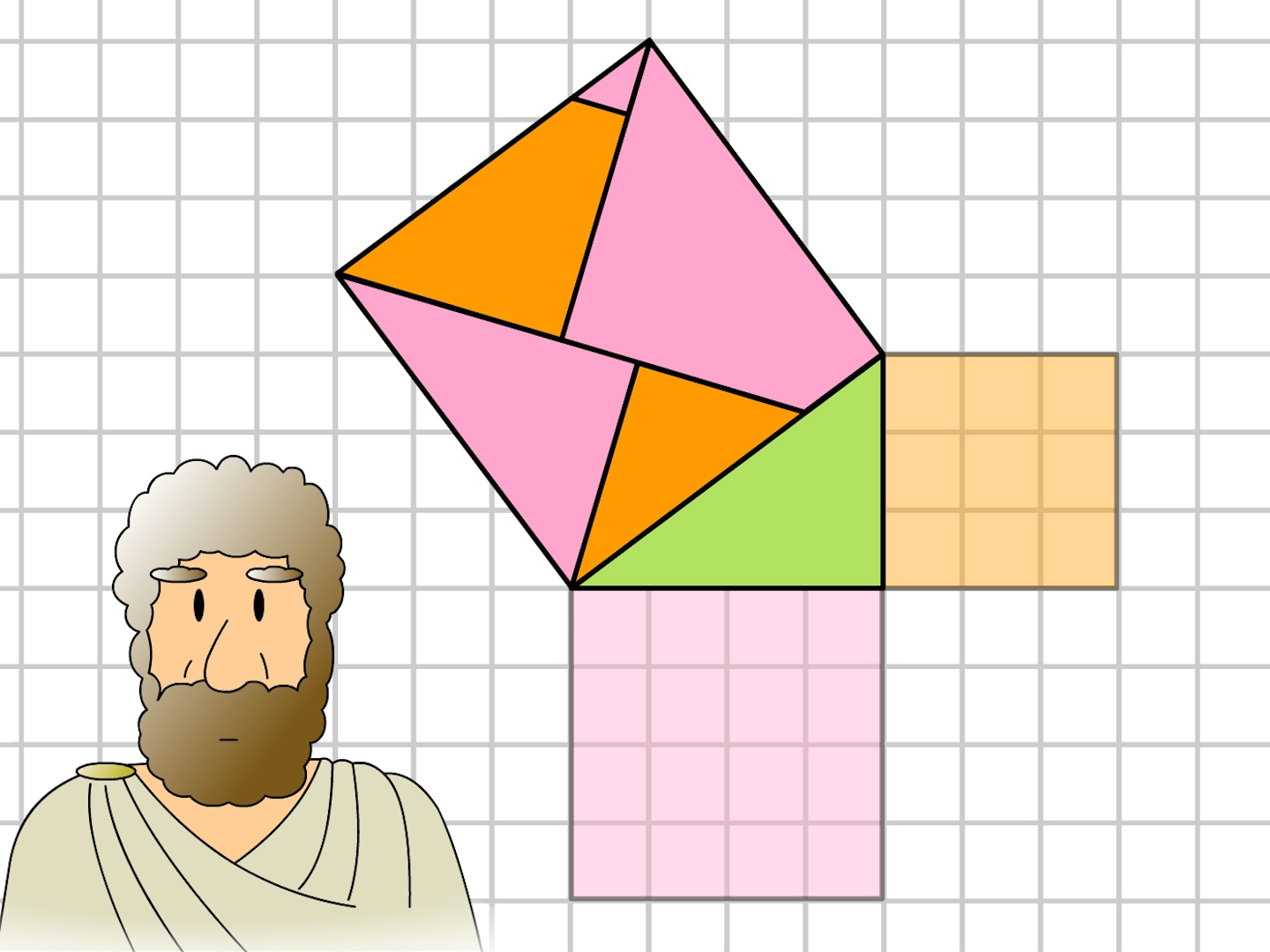
3年 ピタゴラスの定理 数学イメージ動画集 大日本図書

感銘を受けた数学 三平方の定理の美しき証明たち 大人のための数学教室 和 Note
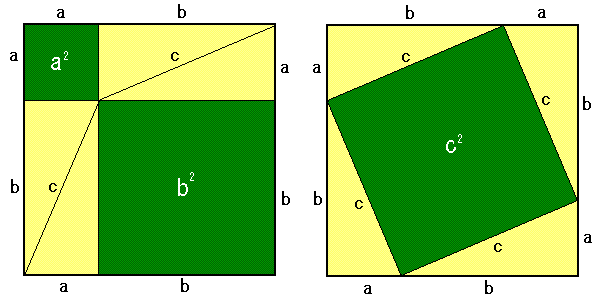
三平方の定理

見えますか タイルの模様からピタゴラスの定理 Note Board

中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理の4通りの美しい証明 高校数学の美しい物語

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

3年 ピタゴラスの定理 数学イメージ動画集 大日本図書

ピタゴラスの三平方の定理 B2 C2 構成三角形で証明を 三角形 ピタゴラス ピタゴラスの定理
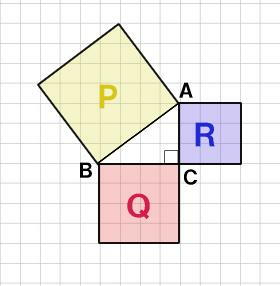
三平方の定理

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

三平方の定理で辺を求める Youtube
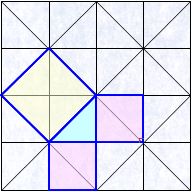
見えますか タイルの模様からピタゴラスの定理 Note Board
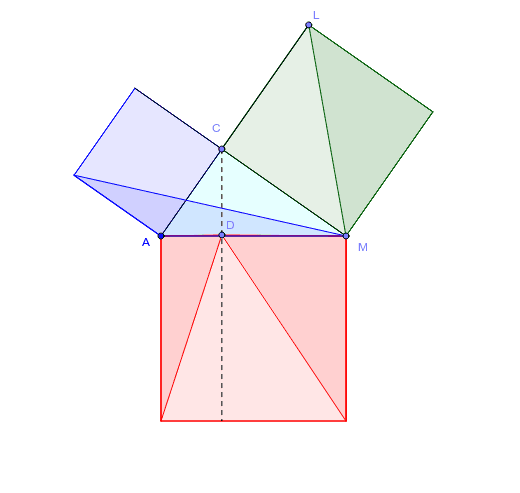
ピタゴラスの定理 ユークリッドの証明 Geogebra

三平方の定理

数学 中3 61 三平方の定理 基本編 Youtube

中学数学 三平方の定理
中学数学 三平方の定理
三平方の定理 ピタゴラスの定理 わかる数学
質問にお答えします 小学生でもわかる数学とは 教育研究所arcs

三平方の定理 ピタゴラスの定理

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット
中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
五角形2 ピタゴラスの定理 Wandering In The Woods
ピタゴラスの定理とその証明

川の対岸までの距離 渡らずに知る方法 働き方 学び方 Nikkei Style
三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

三平方の定理の証明と使い方
三平方の定理とは コトバンク

Lohaco ピタゴラスの定理をめぐる2つの謎 三平方の定理の謎 森下四郎 数学 Bookfan For Lohaco

三平方の定理 ピタゴラスの定理
自然数の組を求める
三平方の定理

三平方の定理 おやじさん ネット

三平方の定理 ピタゴラスの定理 と証明 Rike English

三平方の定理 無料で使える中学学習プリント
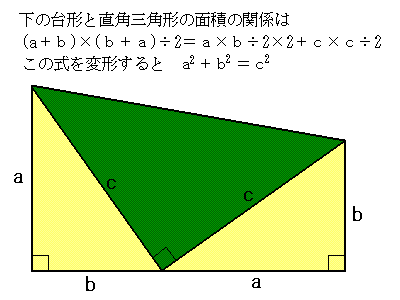
三平方の定理
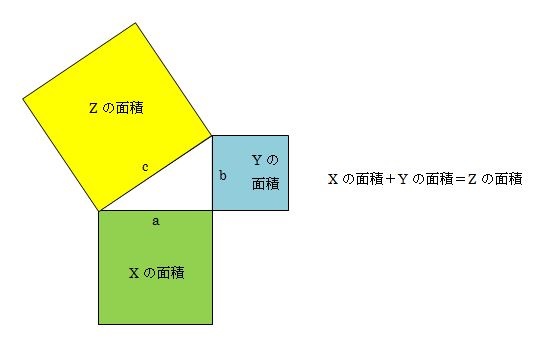
三平方の定理 もう一度やり直しの算数 数学
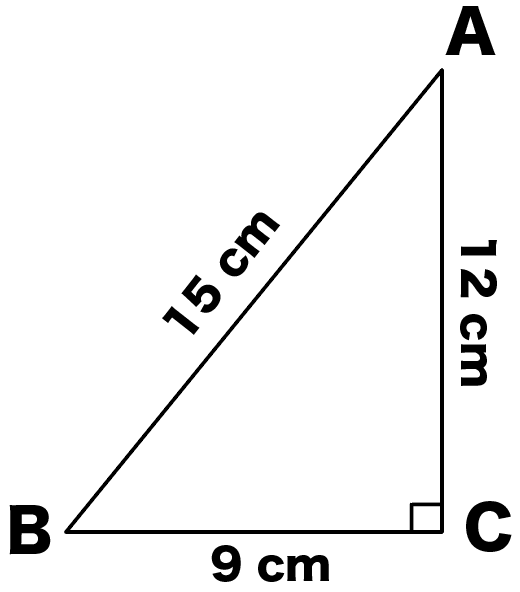
3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト
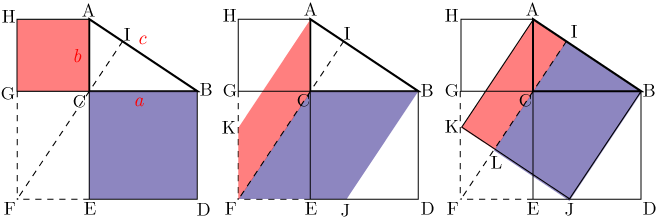
三平方の定理 ピタゴラスの定理

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理の証明と使い方

三平方の定理 ピタゴラスの定理 誕生秘話と証明 永野裕之のblog

三平方の定理の証明 正方形の面積を使う方法 数学教材

これなら小学生でも分かる 水で車輪を使って ピタゴラスの定理 を証明する実験動画 コモンポストムービー

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
三平方の定理の4通りの美しい証明 高校数学の美しい物語
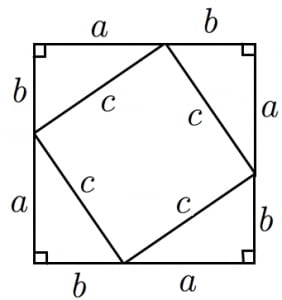
三平方の定理の4通りの美しい証明 高校数学の美しい物語
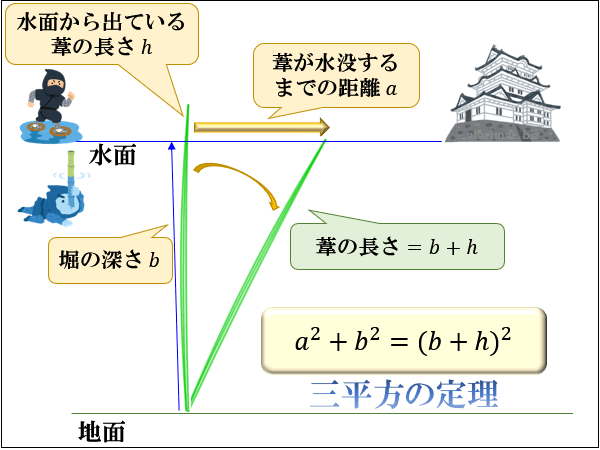
三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ
Q Tbn And9gcsro3fhnelkqc08jeqpmvfwcrxrevhl 8ilyfrxnxocieapnzht Usqp Cau
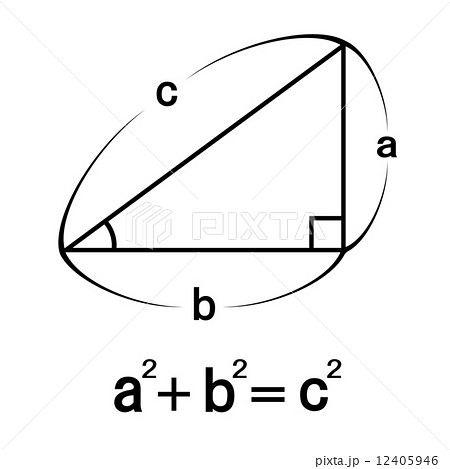
三平方の定理のイラスト素材

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理とsin 2 Cos 2 1の違い たとえば次のような問題 Sina 2 数学 教えて Goo



