三角形 比 定理
3:4:5の三角形で,本当に直角ができるのでしょうか。 三角形の辺の長さの比と角の大きさには,どんな関係があるのでしょうか。 3:4:5は,斜辺の対角が直角です。このことは,三平方の定理として知られています。 3:4:5 ….
![]()
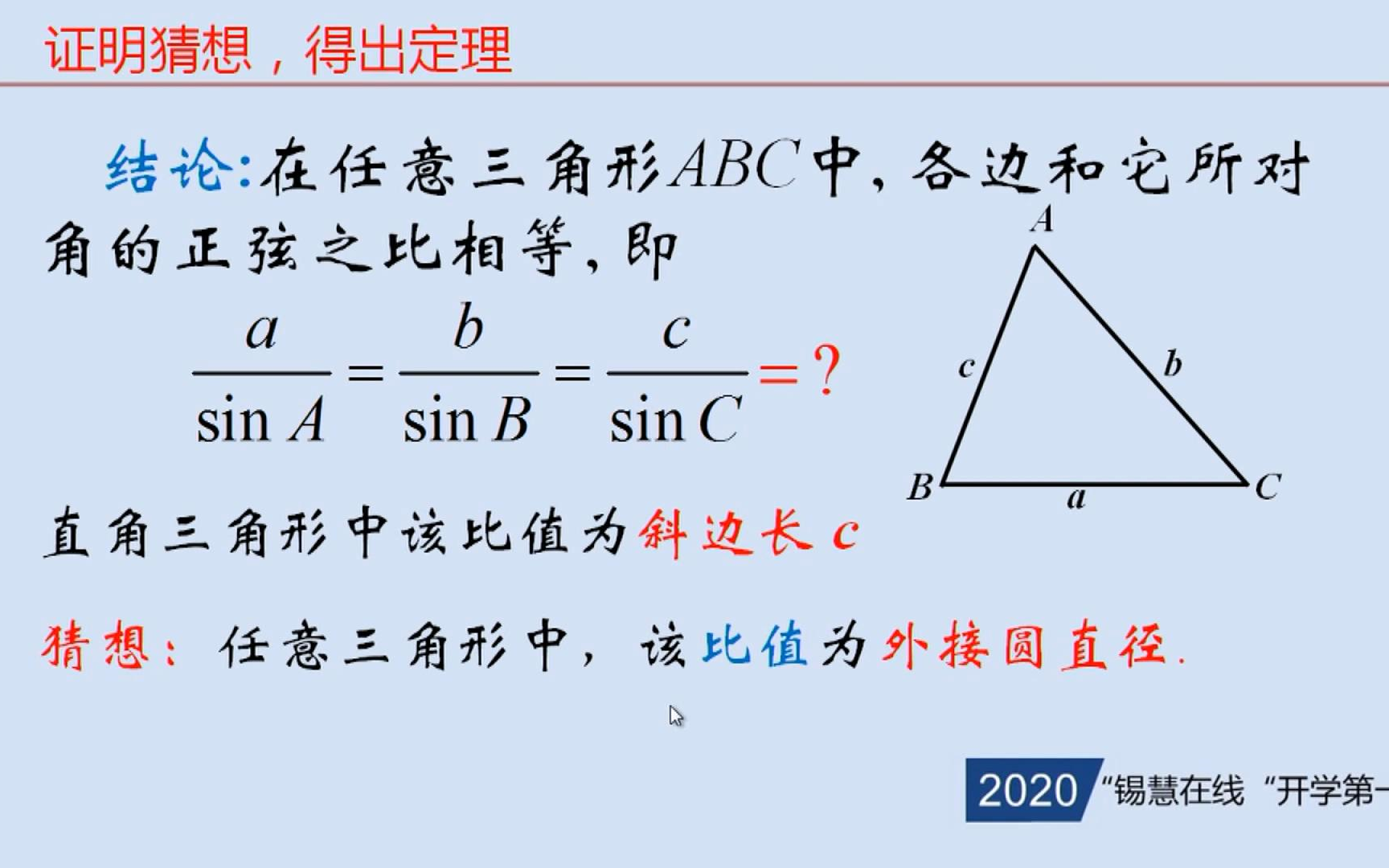
三角形 比 定理. 正弦定理(The Law of Sines)是三角学中的一个基本定理,它指出“在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径”,即a/sinA = b/sinB =c/sinC = 2r=D(r为外接圆半径,D为直径)。. A b c d e abcの辺ab,ac上の点をそれぞれd, eとするとき、 ①de//bcならad:ab=ae:ac=de:bcである。 ②de//bcならad:db=ae:ecである。 ※この定理はd, eが辺ba, caの延長上にあっても成り立つ。 定理の証明 ① abcと adeにおいて de//bcより、平行線の同位角は等しいので. 正三角形を半分にした形って覚えてもらえればいいかな。 中学数学の問題では3秒に一回ぐらい使う直角三角形の辺の比だから、 確実に覚えておこう。 比その2.「1:1:√2」 次の直角三角形の辺の比は、 1 :.
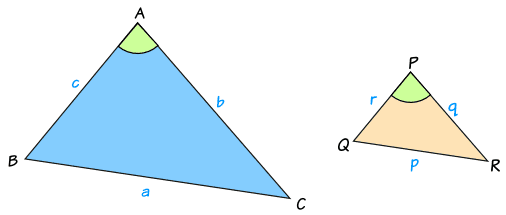
2つの視点から分かる公式の覚え方・考え方 三角形 \(abc\) に対して、点 \(a,b,c\) の内角をそれぞれ角 \. 数学おじさん 今回は、チェバの定理を使える図形を、 チェバの定理を使わずに、解いてみようかと思うんじゃ 具体的には、以下の問題じゃ 数学おじさん 上の図で、 af :. ここでは、三角比の関係式から、三角形の形状を答える問題を考えます。角度は考えづらいので、正弦定理や余弦定理を使って、三角比を辺による表現に変えて考えていきます。 なお、 $ mathrm{ AB }=c$, $ math.
次に,メネラウスの定理を使って, abc の内部の線分の長さの比を求める. メネラウスの定理では,三角形と交わる直線の長さの比は出てこずに,直線によって分けられる三角形の辺の比が出てくることに注意. Triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。. Ce = 1 :.
2 のとき、 bd :. 三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角二等辺三角形タイプです。 これは「正方形半分タイプ」という名前でも覚えておきましょう。. 三角形の一辺に平行な直線をひいた時にできる線分の比 について考えていこう。 辺AB を 4等分 するように 点D、E、F をおいてある。 直線は 3点 から 辺BC に平行になるようひいてあるよ。.
先ほど確認したとおり、三角形の面積は「(底辺)×(高さ)×$\frac{1}{2}$」です。 底辺の比は、相似比なので、1:2。 高さの比も相似比と同様に1:2ですね。 どちらの三角形の面積も$\frac{1}{2}$をかけるので、 ABC: A’B’C’=1×1:2×2=1=4となります。. 三角比の定義は先にお伝えしました直角三角形を用いたものと、 原点を中心とする円を用いたものがあります。 原点中心の円を半径\(\,1\,\)の 単位円 に限定して定義しておきます。. これは、半径Rの円に内接する三角形の辺の長さと、反対側にある角の正弦(sin)の関係を式で結んだものです。 今、下の図のようになっているとき、2R=a/sinA =b/sinB =c/sinC.
この記事では、「直角二等辺三角形」の定義や公式、辺の長さの比などについて解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね! 目次直角二等辺三角形とは?定義直角二等辺三角形. 成り立つ仕組みも基本的にほぼ同じであるため、この「三角形と比の定理」も「平行線と線分の比の定理」と表すことが多いです。 つまり、 区別する必要はない ということですね。. 傍心:傍接円の中心 ※傍心・傍接円は3つある。 定理 外心.
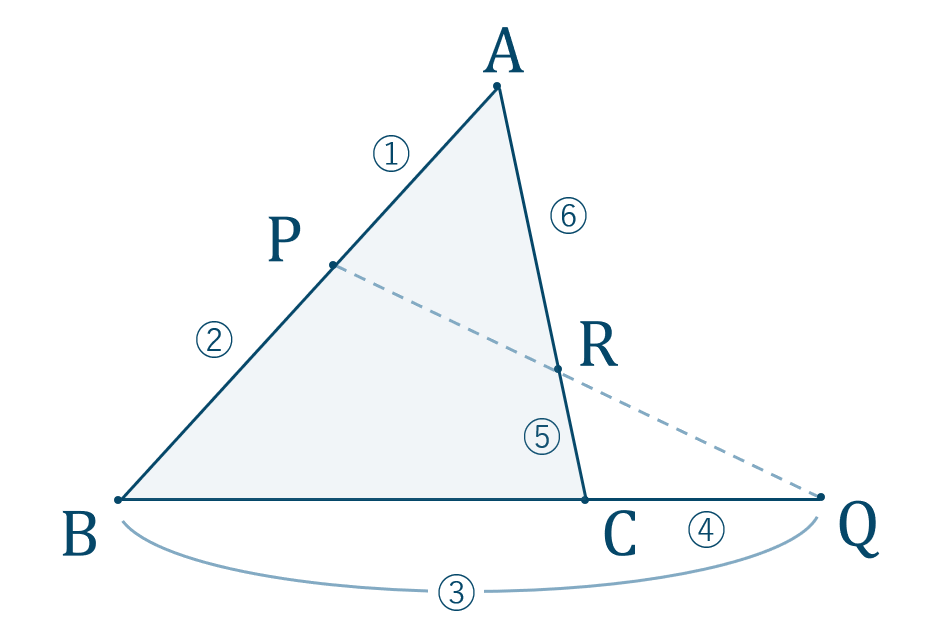
三平方の定理を使って直角三角形の辺の長さを計算したい! どうも、Drリードだぞい。 中3数学では、 三平方の定理(ピタゴラスの定理)を勉強してきたよな? 簡単に復習すると、. 三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。. 三角形の面積を引き算する (4) に進みます。 考え方としては、三角形全体の面積から pqr の周りにある 3 つの三角形の面積を引くことで求めます。 bcq の面積は (3) で求めたので、次に car を求めます。.
この記事では、「二等辺三角形」の定義や定理、性質についてまとめていきます。 辺の長さや角度、面積や比の求め方、そして証明問題についても詳しく解説していくので、一緒に学習していきましょう! 目次二等辺三角形とは?定義. Cd はなんでしょうか? トンちゃん チェバの定理を使えばいいのに、 なぜ、わざわざ. Bf = 3 :.
この上図の三角形より AD の辺の長さを求めます。.

三角形相似定理 相似三角形定理的证明 相似三角形判定定理 相似三角形证明

日本eju留考数学精讲丨三角形内角平分线定理的证明方法 哔哩哔哩 つロ干杯 Bilibili
基础数学 七 几何性质及定理 石天放 博客园
三角形 比 定理 のギャラリー

由边的数量关系识别直角三角形 定理的应用 16 2由边的数量关系识别直角三角形 初中冀教版 数学中国网
相似三角形定理

初中数学相似三角形定理归纳 史上最全就在这里 新东方论坛
几何基础 三角形之重心分中线为2比1 腾讯视频
Q Tbn And9gcsl1rsekpo Zn9wqo9mzgfoueqvlryd5wk2pw Usqp Cau
.png)
打印预览

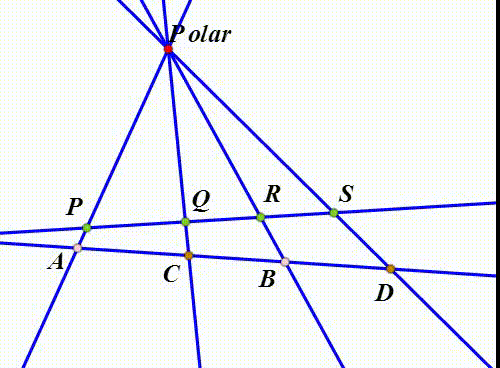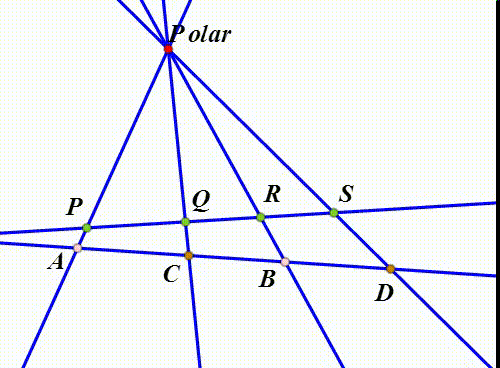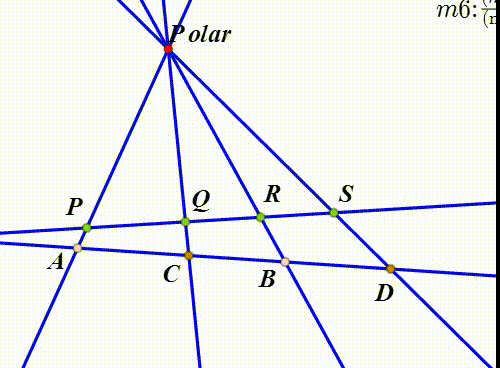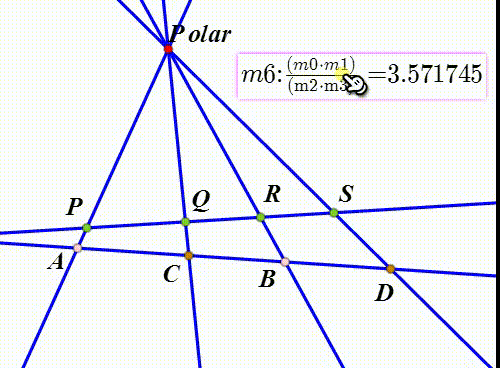
截线定理 维基百科 自由的百科全书

Amc10 数学中的面积公式推证

三角面积鹭公式毕达哥拉斯定理几何 三角形png图片素材免费下载 图片编号 Png素材网
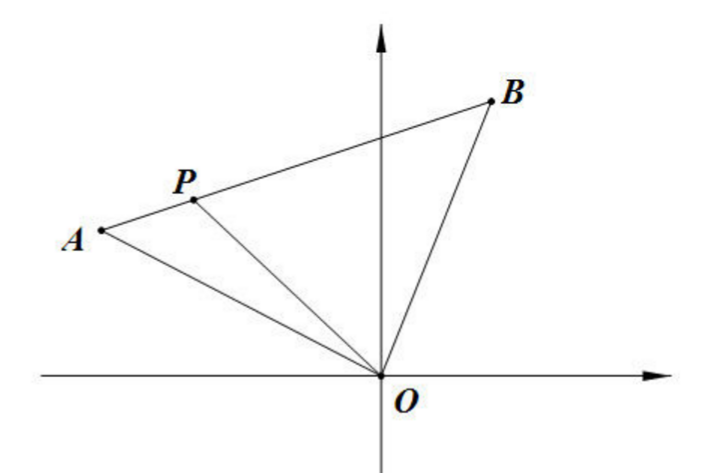
定比分点公式及定理 知乎
三角形角平分线 内角平分线定理的多种证明方法
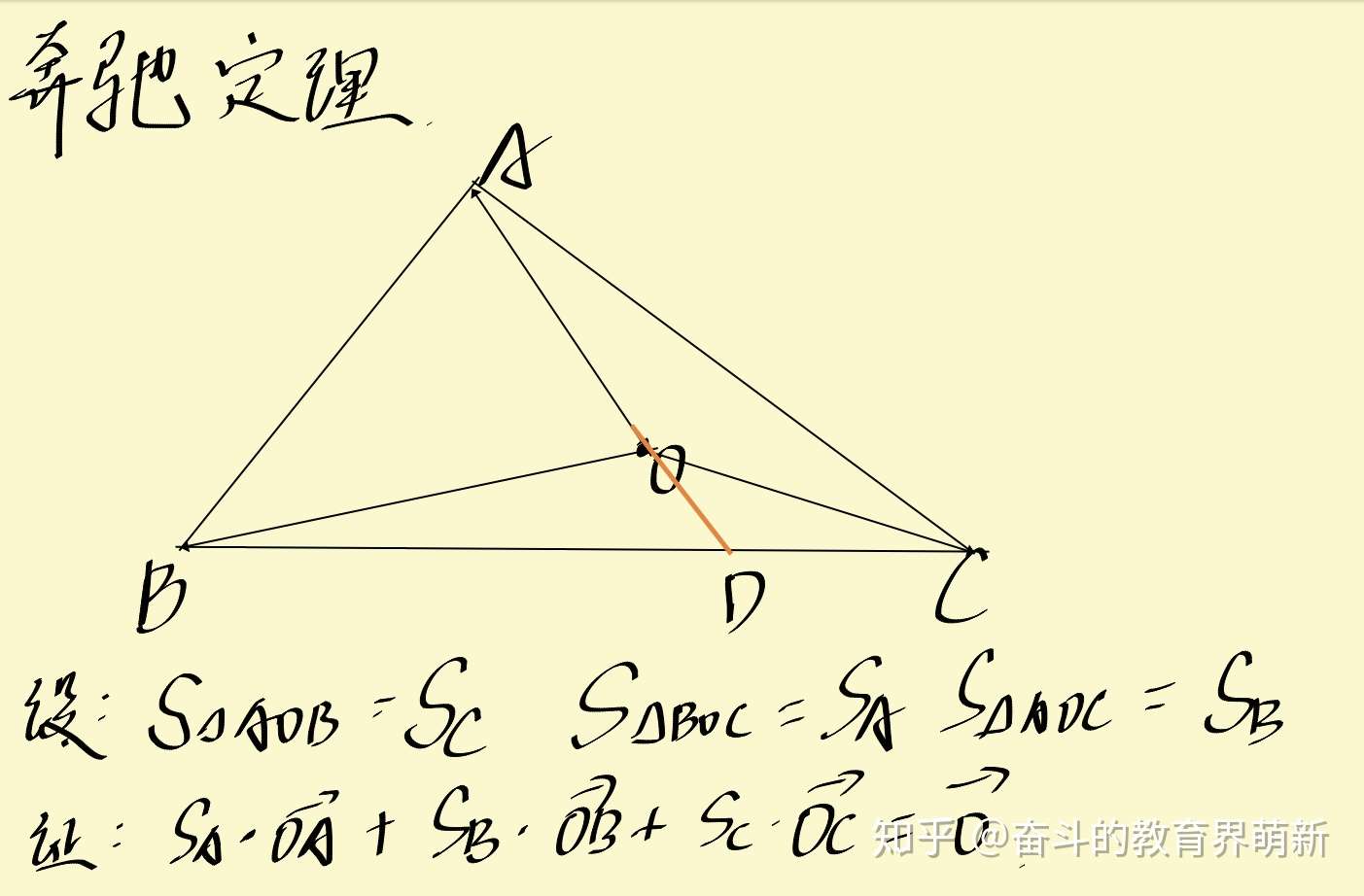
数学杂谈之奔驰定理 知乎

试图将一个数学定理证明到最底层的数哲原理 全栈空间 Csdn博客

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 ベネッセコーポレーション
更好的蝴蝶定理 腾讯视频
高一数学 2月10日 正弦定理1 哔哩哔哩 つロ干杯 Bilibili

试图将一个数学定理证明到最底层的数哲原理 全栈空间 Csdn博客

平面几何相关定理 静雅斋数学 博客园

7 利用畢氏定理求三角比的值 Youtube
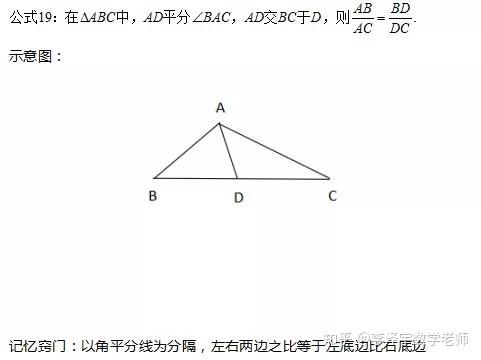
那些让你加快解题速度的高中数学公式 19 三角形内角平分线性质定理 知乎
张景中院士批教育部负面清单 禁初中生学小学生都可以理解的知识点 和乐数学 微信公众号文章阅读 Wemp

蝴蝶定理模型和相似模型 小學數學競賽模型 每日頭條

三角形一边的平行线性质定理 完全不理解 真的很难去想清楚 定理是这样的 平行与三角形 一边的直线截其他两边所在的直线 截得的对应线段成比例 一条直线截另一条直线 截直线怎么 作业 慧海网
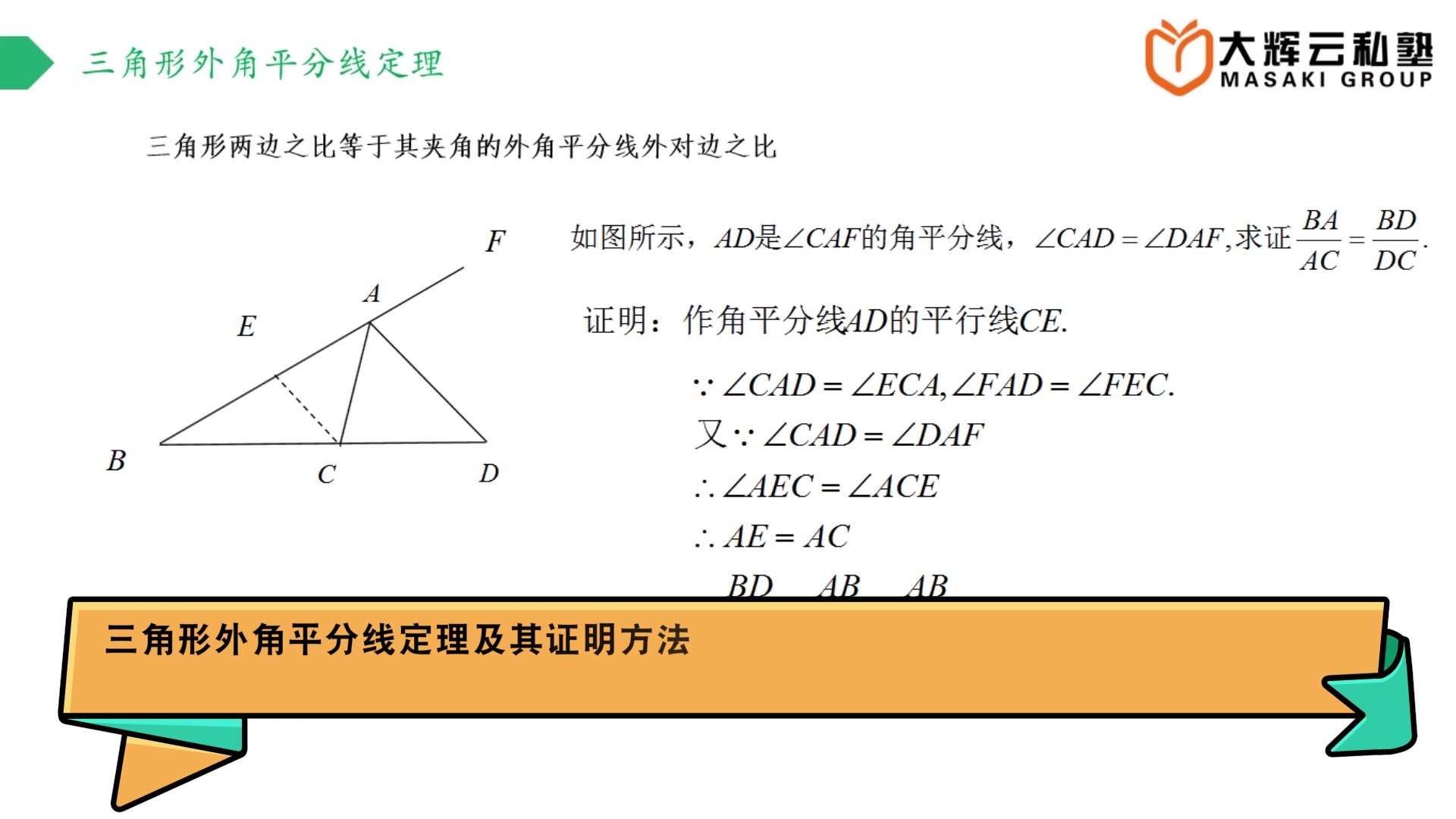
日本eju留考数学丨1分钟带你学会三角形外角平分线定理及其证明方法 哔哩哔哩 つロ干杯 Bilibili

初中几何五大模型 学会轻松搞定初中几何 考试不再愁 每日头条

中学数学 三角形と比

相似三角形问题解法 初中数学常用解题方法 每日头条

截距定理线段三角形比 分界线png图片素材免费下载 图片编号 Png素材网

小升初数学重点 鸟头定理 每日头条
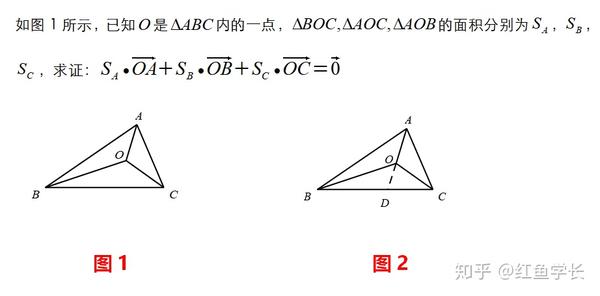
高考有哪些快速解题技巧 奔驰定理 了解一下 选择填空拿满分 知乎
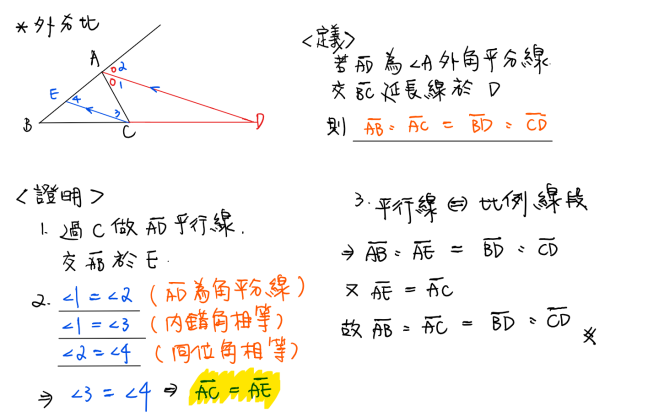
三角形內分比 外分比定理 Easy Math Club
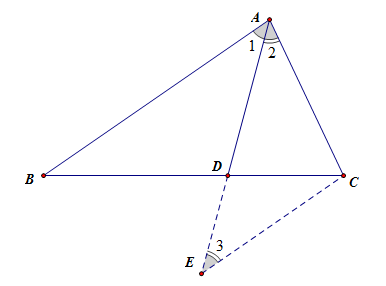
平面几何相关定理 静雅斋数学 博客园
正弦定理和余弦定理 天奇教育
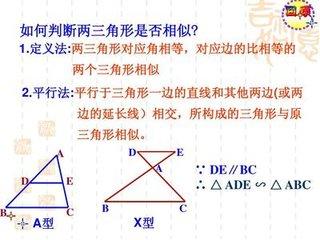
初中几何 相似三角形的判定 定理知识点归纳总结例题讲解基础练 初中数学 学习资料大全 免费学习资源下载

数学杂谈之奔驰定理 知乎
Q Tbn And9gcsept Argmyfiduzxsvlb6qcgahxwthxbh 2w Usqp Cau

三角形平行线定理 第1页 一起扣扣网

常見的直角三角形之三邊長比 畢氏數 勾股數 Live 多媒體數學觀念典online

刘伟业 知乎

三角法恒等式
Q Tbn And9gctqgzcv5lv7plcaixkm0qyotxshvkr1w4zpyw Usqp Cau

三角形と比の定理の逆 中学生 数学のノート Clear

高考数学向量奔驰定理应用秒解三角形面积比问题 哔哩哔哩 つロ干杯 Bilibili

相似三角形的判定定理
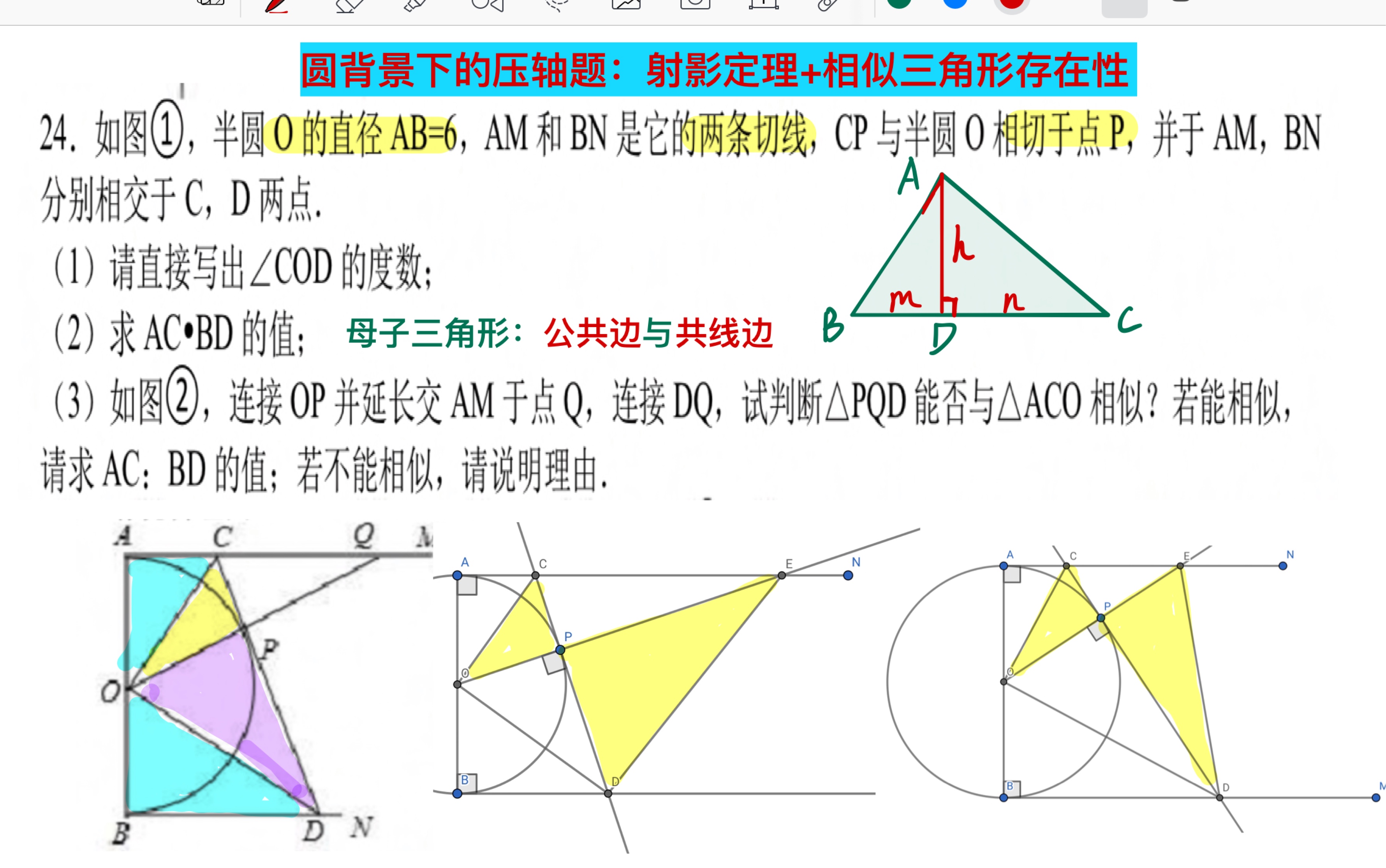
圆 挑战压轴题 射影定理 相似三角形存在性 哔哩哔哩 つロ干杯 Bilibili

三角形截距定理泰勒斯定理数学 三角形png图片素材免费下载 图片编号 Png素材网
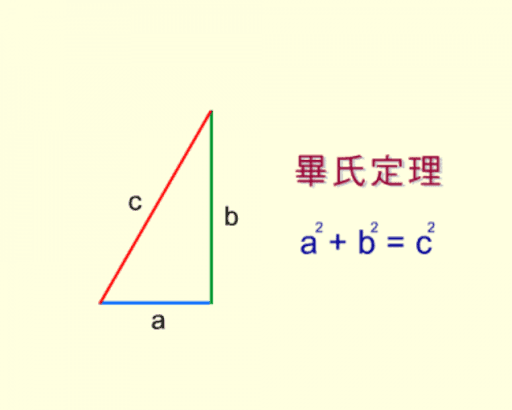
畢氏定理 勾股定理 Pythagorean Theorem Geogebra

三角形平行线定理 第1页 一起扣扣网

比例线段 相似三角模型比例线段

三角形面积的五种典型算法 简书

初中数学相似三角形知识点 经典例题整理 每年中考都会考 每日头条
相似三角形定理

角平分线定理和直角三角形的射影定理 图文 百度文库

角平分定理直角三角形 三角形png图片素材免费下载 图片编号 Png素材网
相似三角形定理
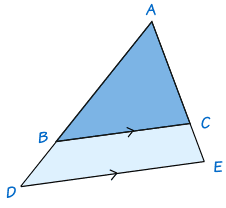
相似三角形定理
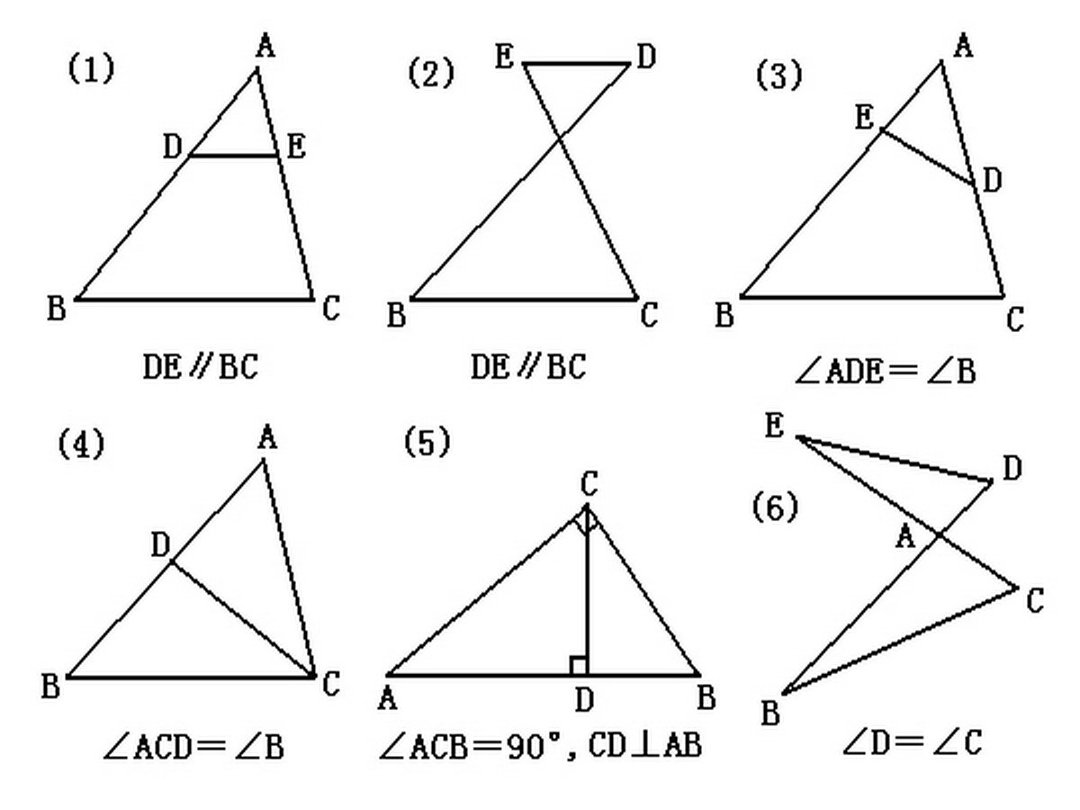
相似三角形判定定理 360百科

常見的直角三角形之三邊長比 畢氏數 勾股數 Live 多媒體數學觀念典online

初中生真的能理解这个 如何利用交比秒证坎迪定理 哔哩哔哩 つロ干杯 Bilibili
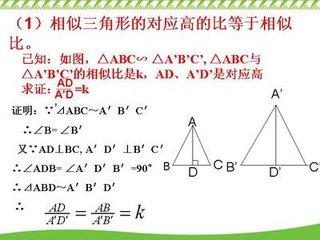
初中几何 相似三角形的判定 定理知识点归纳总结例题讲解基础练 初中数学 学习资料大全 免费学习资源下载
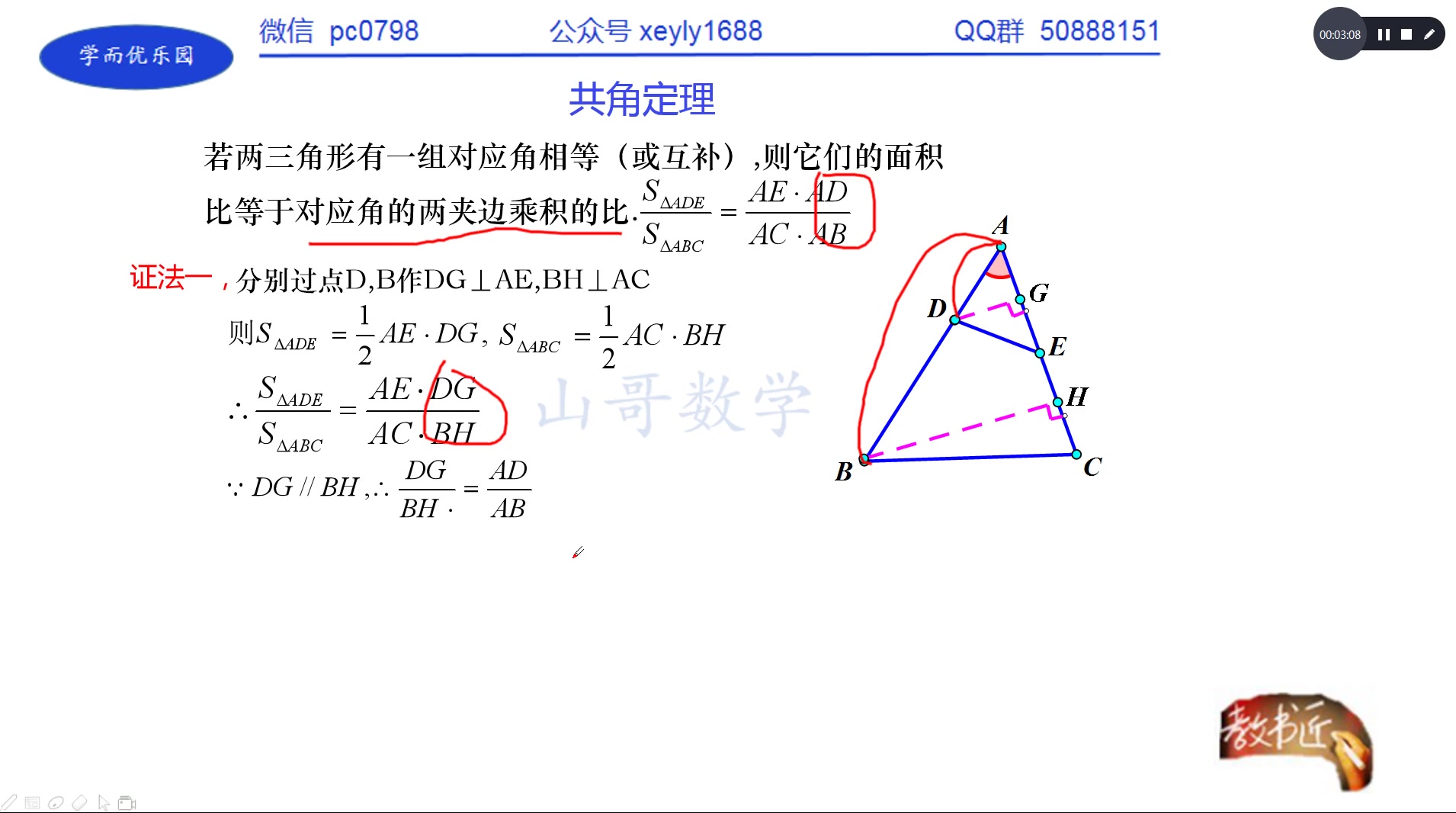
8 角平分线第二定理 哔哩哔哩 つロ干杯 Bilibili

小学阶段三角形问题五大模型 实题实练 每日头条
公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学
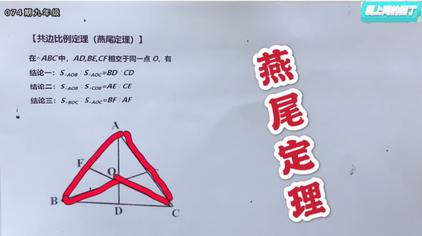
燕尾定理视频在线观看 西瓜视频

相似三角形预备定理 百度文库
基础数学 七 几何性质及定理 石天放 博客园
相似三角形判定定理 定理内容 性质定理 判定方法 头条百科
平行线分线段成比例定理 头条百科

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

比费马大定理还难的数 数学家证明1不是同余数 花了一千多年 每日头条
相似三角形定理

截距定理线段三角形比 三角形png图片素材免费下载 图片编号 Png素材网
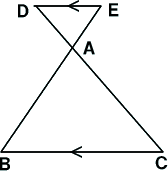
三角形と比

平面几何相关定理 静雅斋数学 博客园

比费马大定理还难的数 数学家证明1不是同余数 花了一千多年 快资讯

三角形元素外角定理内角三角形png图片素材免费下载 图片编号 Png素材网
壁紙押入れ 最高三角形比定理

助力中考数学 手拉手旋转 相似问题怎么解

Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎
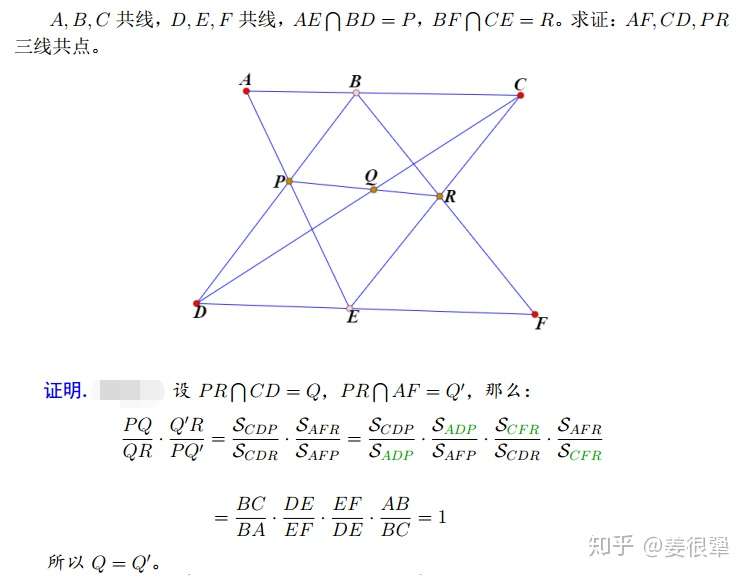
面积消点法 知乎

中学数学 三角形と比
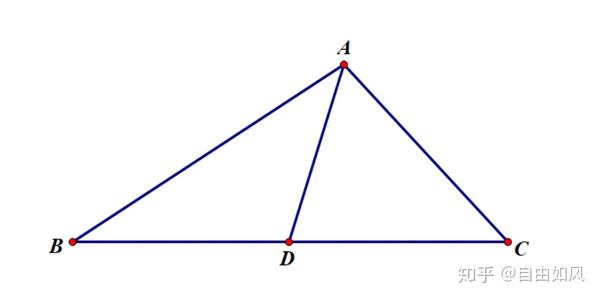
0 4 几个平面几何中常见定理 知乎

相似三角形面积比和边长比的关系相似三角形的判定 知识点 就上高考网
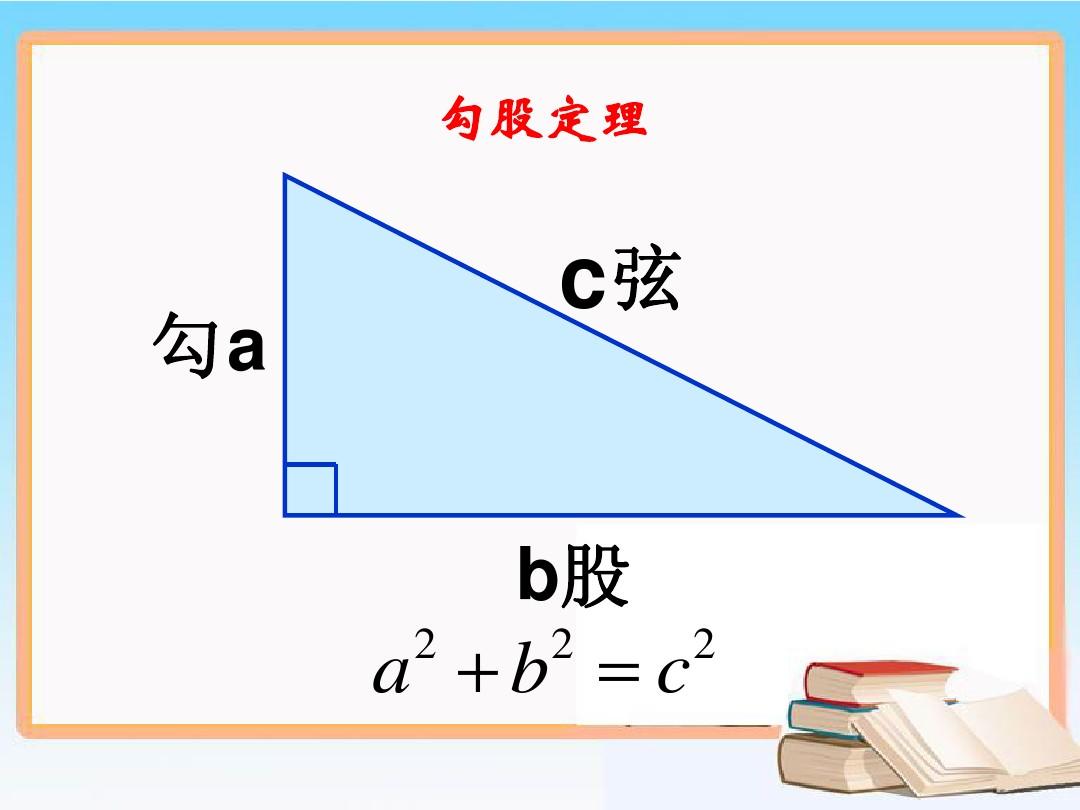
中国的勾三股四弦五比西方晚了多少年 周髀算经 数组 定理 新浪新闻

常見的直角三角形之三邊長比 畢氏數 勾股數 Live 多媒體數學觀念典online

截距定理thales定理三角形pythagorean定理 三角形png图片素材免费下载 图片编号 Png素材网
常見的直角三角形之三邊長比 畢氏數 勾股數 Live 多媒體數學觀念典online
Q Tbn And9gcsatfsg4cduqioclfc3414mn Bueh8tiujpqwnri1dr A8m1n Usqp Cau
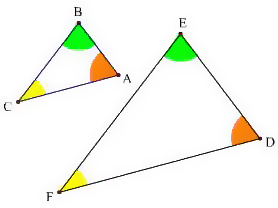
相似三角形 维基百科 自由的百科全书
几何课关于三角形你不得不记住的定理 从勾股定理到托勒密定理

三角形内角和拼接图片 第1页 一起扣扣网

试图将一个数学定理证明到最底层的数哲原理 全栈空间 Csdn博客

Ceva定理三角形数学点三角形png图片素材免费下载 图片编号 Png素材网
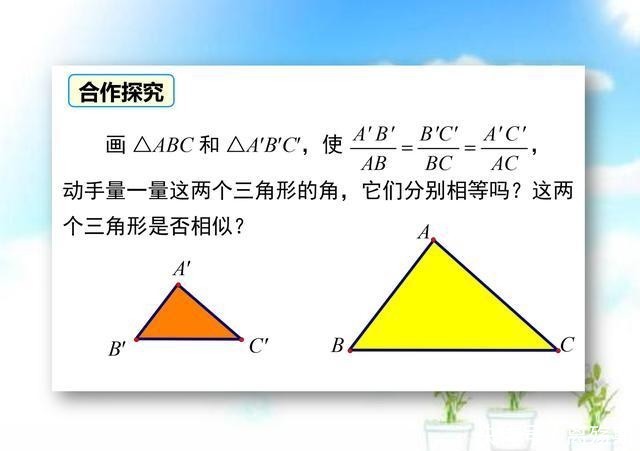
四十五度三角形三边比例

18 塞瓦定理 简书

截距定理thales定理三角形平行三角形png图片素材免费下载 图片编号 Png素材网

三角形內分比 外分比定理 Easy Math Club

毕达哥拉斯定理三角形数学空间对角三角形png图片素材免费下载 图片编号 Png素材网



